Hidden Markov Model
An introduction to Hidden Markov Model
Hidden Markov model (HMM) là một mô hình xác suất dựa trên nhiều Markov chain.
Markov chain
Markov chain có thể coi là một sơ đồ chuyển trạng thái mà trong đó các node là trạng thái(có thể là một từ, hoặc là một giá trị từ một tập nào đó) còn các cạnh có trọng số là sác xuất chuyển trạng thái.
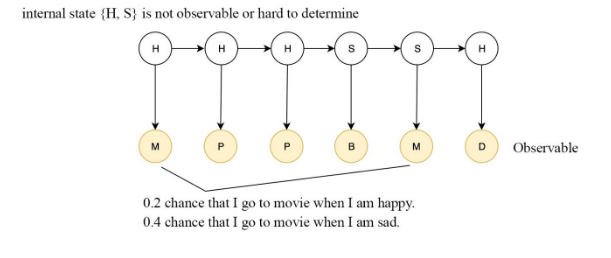
Markov chain rất hữu dụng trong việc tính toán xác suất của một chuỗi sự kiện. Trong nhiều trường hợp, chúng ta không thể quan sát đc các sự kiện đó, hoặc không thể quan sát nó một cách trực tiếp. Ví dụ trong việc gán POS cho một đoạn văn bởi vì chúng ta không thể quan sát đc các tag chính xác cho từ là gì.
Mô hình HMM
HMM tìm các giá trị hoặc xác xuất của các sự kiện ẩn dựa trên các biến quan sát được. Mô hình HMM sẽ bao gồm các thành phần :
- Q = [q1, q2, q3,…]: là một tập hợp các trạng thái.
- O = [o1, o2, o3,…]: là một tập hợp các quan sát.
- A = [a11, …, aji, …, aNN]: là ma trận chứa xác suất chuyển trạng thái của các trạng thái trong Q
- B = bi(ot): là ma trận xác suất phát thải của một quan sát ot được tạo từ một trạng thái i
- pi = [pi1, pi2, pi3, …]: là phân phối xác suất khởi tạo

Trong HMM trạng thái tiếp theo và quan sát hiện tại phụ thuộc vào trạng thái hiện tại. Cho nên với tất cả quan sát và trạng thái khởi tạo chúng ta có thể tính toán trạng thái tại một thời điểm t.

Xác định trạng thái tại thời điểm cụ thể - Foward Algorithm
Trong HMM chúng ta tìm trạng thái tại thời điểm t bằng cách sử dụng trạng thái tại thời điểm t-1 hoặc t+1.
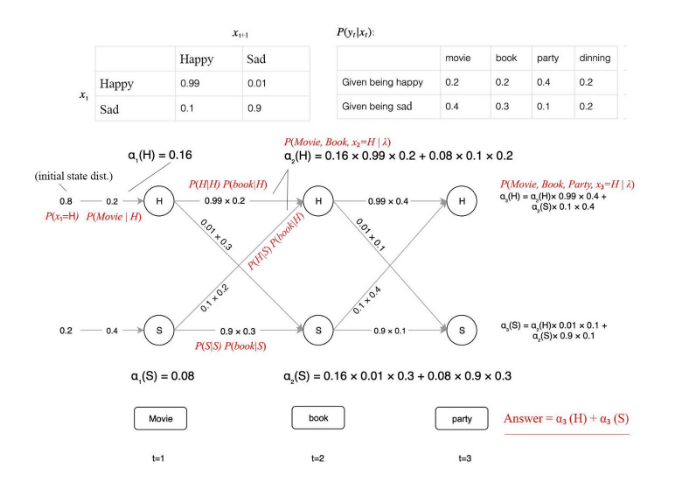
Như hình ví dụ bên trên, bạn có thể thấy. Xác suất tại mỗi node được tính bằng cách tính tổng của tất cả các đường đi có thể dẫn tới node đó. Cho qt = j là trạng thái tại thời điểm t.
Viterbi
Tìm trạng thái tối ưu cho một chuỗi quan sát còn gọi là quá trình Decode. Cho trạng thái j tại thời điểm t, vt(j) là xác suất chung của chuỗi quan sát và chuỗi trang thái tối ưu nhất. Ta sẽ có công thức như sau:
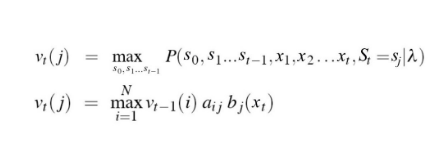
Vì Viterbi là sử dụng quy hoạch động nên rất tối ưu cho bài toán đi tìm chuỗi tối ưu nhất. Bởi vì chúng ta không tính xác suất của tất cả.